AKKD

1. Dyscypliny, klasy, filtry
2. PRIO
3. CBQ
   1. Teoria
   2. Estymator i Planista
   3. Szczegóły implementacji
   4. Wykorzystanie
4. HTB
   1. Początki
   2. HTB 3
   3. Wykorzystanie
5. H-FSC
   1. Wstęp
   2. Krzywa usługi
   3. Sposób działania HFSC
   4. Deadline i Eligible time
   5. Virtual time
   6. Szczegóły implementacji
   7. Wykorzystanie

Krzywa usługi

Pojęcie ,,krzywa usługi'' (ang. ,,service curve'') wprowadził Rene Cruz [1]. Mówi się, że połączenie (klasa) $i$ ma zagwarantowaną krzywą usługi $S_i(t)$, jeśli dla każdej chwili $t_2$ istnieje taka chwila $t_1 < t_2$, w której miał miejsce początek zaległości tego połączenia (klasy) oraz zachodzi: $$ S_i(t_2-t_1) \le W_i(t_1,t_2) $$ gdzie $W_i(t_1,t_2)$ to ilość usługi otrzymana przez połączenie (klasę) $i$ w czasie $(t_1, t_2]$. Obrazowo mówiąc, krzywa usługi ogranicza przepływność danych do wiadra żetonów z tą różnicą, że ograniczenie nakłada się ,,od dołu''. To znaczy, że jeśli tylko połączenie ma wystarczająco danych do przesłania, to dane te nie będą przesyłane wolniej niż określa to krzywa (patrz rys.).

Przykład krzywej usługi. Zaznaczone maksymalne zaległości (pionowo)
oraz maksymalna wielkość opóźnienia (poziomo).
Według: Rene L. Cruz ,,Quality of Service Guarantees in Virtual Circuit Switched Networks'',
IEEE JOURNAL IN COMMUNICATION, sierpień 1995

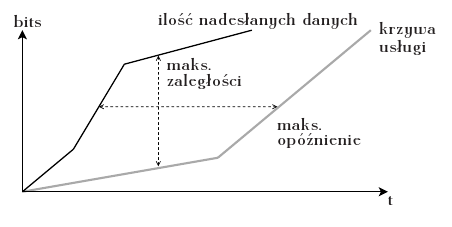Algorytm ważonego sprawiedliwego kolejkowania (WFQ) da się opisać liniowymi krzywymi usług (a więc można powiedzieć ,,prostymi usług'') przecinającymi środek układu współrzędnych (ilości usługi do czasu). Dla każdego połączenia spełniony jest warunek: $$W_i(t_1,t_2) \ge \phi_i W(t_1,t_2)$$ gdzie $W(t_1,t_2)$ to ilość usługi dostarczana przez całość łącza, a $\phi_i$ to udział przydzielony połączeniu.

Jednym z pierwszych algorytmów używających koncepcji krzywych usług jest SCED (Service Curve Earliest Deadline first). Dla każdego połączenia $i$ obliczany jest oddzielnie nieprzekraczalny (ostateczny, ang. deadline) czas wysłania kolejnego pakietu. W wyidealizowanym modelu, połączenie $i$ w każdej chwili $t$ będzie miało zagwarantowane, że otrzymało przynajmniej $D_i(t)$ usługi. Krzywa $D_i(t)$ obliczana jest w następujący sposób. Kiedy na połączeniu pojawiają się pierwsze zaległości (jakiekolwiek pakiety do wysłania), $D_i(t)$ jest inicjowana według przydzielonej połączeniu krzywej usługi $S_i(t)$. Następnie, kiedy na połączeniu tworzą się kolejne zaległości (oznaczmy tą chwilę jako $t_1$), krzywa $D_i(t)$ jest aktualizowana: $$ D_i(t) = min(D_i(t), S_i(t-t_1) + W_i(t_1)) ~~~ \textrm{dla każdego} ~~~ t > D_i^{-1} (W_i(t_1)) $$ gdzie $W_i(t_1)$ jest całkowitą ilością usługi otrzymaną przez połączenie $i$ do chwili $t_1$, a $D_i^{-1}(y) = min(t: D_i(t) = y)$ i $D_i(t)$ jest zdefiniowane tylko dla $t > D_i^{-1}(W_i(t)+L_i^k)$ ($L_i^k$ jest długością pakietu $k$ – następnego do wysłania z połączenia $i$). Krzywa $D(t)$ reprezentuje ilość usługi nie uwzględniając tego, że pakiety muszą być wysyłane w całości. Dlatego czas nieokreślony dla pakietu $k$ obliczany jest według wzoru: $$ d_i^k = D_i^{-1}(W_i(t) + L_i^k) $$ SCED wysyła zawsze ten pakiet, który ma najbliższy czas nieprzekraczalny.

Aby zobrazować jak pomocny może być mechanizm krzywych usług ropatrzmy przykład podany przez twórców H-FSC [2]. Dwa połączenia korzystające z tego samego łącza rozpoczynają transmisje w tym samym momencie (Oczywiście nie zupełnie równocześnie – wystarczy, że oba połączenia dostarczą do urządzenia swój pierwszy pakiet zanim którykolwiek z nich zostanie wysłany). Jedno połączenie nazwijmy Video i niech wymaga niewielkiej przepustowości lecz opóźnienia maksymalnie 10 ms. Drugie połączenie to sesja FTP wymagająca dużej przepustowości lecz nie dbająca praktycznie o opóźnienia.

Mechanizm krzywych usług na przykładzie podziału łącza
między połączeniem wymagającym małego opóźnienia a połączeniem o dużej przepustowości;
A) w algorytmach z liniowymi krzywymi usług (czyli bez wykorzystania krzywych);
B) z wykorzystaniem nieliniowych krzywych usług
Według: dz. cyt.

Problemy z krzywymi usług

SCED podatny jest na nieprzyjemną sytuację, kiedy połączenie wysłało więcej niż gwarantuje jej krzywa usługi (z powodu dostępności pasma), a drugie połączenie nagle dostaje dużo zaległości, które jego krzywa usługi powinna pozwolić mu wysłać (rys. poniżej). Można rzec, że pierwsze połączenie jest wtedy ,,karane'' za zbyt szybkie wysyłanie, albowiem musi czekać tak długo, aż czas nieprzekraczalny drugiego połączenia przerośnie aktualny jego czas nieprzekraczalny. To pierwszy problem z którym H-FSC musiało sobie poradzić.

Pułapka SCED;
A) Krzywe usług $S_1$ i $S_2$ oraz przepustowość łącza (linia przerywana);
B) połączenie $W_1$ o krzywej $S_1$ rozpoczyna wysyłanie;
C) w momencie $t_0$ połączenie $W_2$ o krzywej $S_2$ rozpoczyna wysyłanie
powodując zastój w pierwszym połączeniu aż do czasu $t_1$;
D) Rozwiązanie polegające na przesunięciu krzywej drugiego połączenia
dodatkowo o opóźnienie pierwszego połączenia powoduje niespełnienie krzywej $S_2$
(zaznaczone szarą przerywaną linią);
Według: dz. cyt.

Kolejny kłopot pojawia się w zastosowaniu krzywych usług w hierarchii klas. Określenie krzywych dla każdej klasy pociąga za sobą wymóg, by każda krzywa na ścieżce począwszy od liścia do korzenia była zagwarantowana. Istnieją jednak sytuacje, kiedy nie może on być spełniony (rys. poniżej).

Problem współdzielenia krzywych usług w hierarchii klas;
u góry – krzywe usług w hierarchii, u dołu – dane wysyłane według krzywych;
A) Połączenie z klasy $2$ rozpoczyna wysyłanie danych w chwili $t_0$, czyli nieco później niż reszta połączeń;
B) Aby zagwarantować krzywe dla klas $1$ i $2$ potrzebne jest więcej przepustowości niż gwaranuje to krzywa dla klasy $5$;
C) Suma potrzebnego pasma aby zagwarantować wszystkie krzywe przekracza przepustowość pasma;
Według: dz. cyt.

1. [^] Rene L. Cruz, ,,Service Burstiness and Dynamic Burstiness Measures: A Framework'', JOURNAL OF HIGH SPEED NETWORKS, Uniwersytet Kalifornijski, kwiecień 1992
2. [^] Ion Stoica, Hui Zhang, T. S. Eugene Ng, ,,A Hierarchical Fair Service Curve Algorithm for Link-Sharing, Real-Time and Priority Services'', Carnegie Mellon University Pittsburgh, PA 15213, 1997, ss. 3-4