AKKD

1. Dyscypliny, klasy, filtry
2. PRIO
3. CBQ
   1. Teoria
   2. Estymator i Planista
   3. Szczegóły implementacji
   4. Wykorzystanie
4. HTB
   1. Początki
   2. HTB 3
   3. Wykorzystanie
5. H-FSC
   1. Wstęp
   2. Krzywa usługi
   3. Sposób działania HFSC
   4. Deadline i Eligible time
   5. Virtual time
   6. Szczegóły implementacji
   7. Wykorzystanie

CBQ – Class Based Queueing

Tendencje do klasowego kolejkowania rozpoczął pomysł pierwotnie przedstawiony przez Davida Clarka i Vana Jacobsona w 1991 roku[1] który wyewoluował w tak zwane Kolejkowanie oparte na klasach (Class Based Queueing). Dokładny opis opublikowany został dopiero 4 lata później na łamach IEEE/ACM Transactions On Networking w 1995 roku[2].

Priorytetem podczas tworzenia CBQ było pogodzenie w jednym algorytmie kolejkowania usług czasu rzeczywistego (ang. real-time) z usługami współdzielącymi łącze (ang. link-sharing). Aby to osiągnąć zdefiniowane zostały ograniczenia nakładane na oba typy usług tak, by priorytetowa usługa czasu rzeczywistego nie mogła zatrzymać całkowicie usługi o niższym priorytecie, a jednocześnie sama nie ucierpiała. W szczególności, algorytm powinien umożliwić sytuację (rys. poniżej), w której podczas przeciążenia niektóre usługi mogą być zatrzymane a niektóre powinny dostawać pewien minimalny przydział. Na przykład usługi asynchroniczne takie jak chociażby poczta elektroniczna mogą być zatrzymane nawet na dłuższy czas (np. kilka minut) nie powodując zauważalnego spadku jakości usługi. Algorytm powinien też pilnować by nadmiar dostępnego pasma był rozkładany hierarchicznie między klasami według odpowiednich wag.

Minimalne przydziały w klasach podczas przeciążenia łącza.

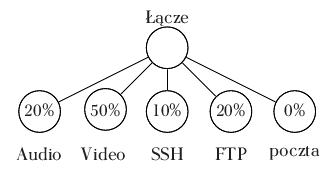Koncepcja współdzielenia

Konceptualny model algorytmu zawiera szereg pojęć, których reprezentacje niekoniecznie muszą wystąpić w implementacji, ale ich opis pozwala na bardziej formalne zdefiniowanie zasad działania.

• Planista generalny i współdzielący (ang. General and link-sharing scheduler, selector oraz delayer u Clarka i Jacobsona) – Klasy posiadają własne kolejki (wirtualne czy rzeczywiste – pozostaje kwestią implementacji) z których pakiety zdejmowane mogą być na dwa sposoby: według planisty generalnego lub współdzielącego.
  • Planista generalny zdejmuje pakiety w sposób zależny od implementacji (np. według algorytmu karuzelowego); jest używany jeśli łącze nie jest wykorzystywane w pełni (każda klasa ma możliwość wykorzystania dodatkowego pasma);
  • Planista współdzielący jest wywoływany w momencie wykorzystania całości łącza; działa on na rzecz klas, które używają więcej pasma niż zostało im przydzielone – decyduje o tym zasada współdzielenia; planista ten limituje prędkość wysyłania klas zgodnie z określonymi zasadami (np. wagami) współdzielenia.
• Klasy regulowane i nieregulowane – Mówimy, że klasa jest regulowana, jeśli pakiety z jej kolejki mają być zdejmowane przez planistę współdzielącego, natomiast nieregulowana, jeśli przez planistę generalnego.
• Estymator – Sposób obliczania aktualnego tempa wysyłania danych przez daną klasę. Estymator decyduje kiedy przałączać klasę w tryb regulowany lub nieregulowany; powienien też brać pod uwage zapełnienie łącza.
• Limit (ang. overlimit, underlimit, at-limit) – Mówimy, że klasa jest nad limitem, jeśli wysłała ostatnio więcej niż wynosił jej przydział współdzielony; pod limitem, jeśli wysłała mniej niż określony ułamek jej udziału; a w przeciwnym wypadku jest na limicie. Stany te ustawia estymator.
• Klasy spełnione i niespełnione (ang. satisfied and unsatisfied classes) – Klasa jest niespełniona jeśli jest pod swoim limitem oraz ma zaległości (Autorzy nie definiują dokładnie co to oznacza pozostawiając to implementacji; przyjmuje się, że oznacza to, iż w jej kolejce czekają pakiety; por. Pomiar Golestaniego, a spełniona w przeciwnym wypadku).
• Poziomy – Klasom przyporządkowane są poziomy według następującego schematu: Klasy liście otrzymują poziom $1$. Każda klasa niebędąca liściem otrzymuje poziom o jeden większy niż najwyższy poziom z wszystkich jej dzieci.

Przypadki występujące podczas działania algorytmu CBQ; wg. [2]

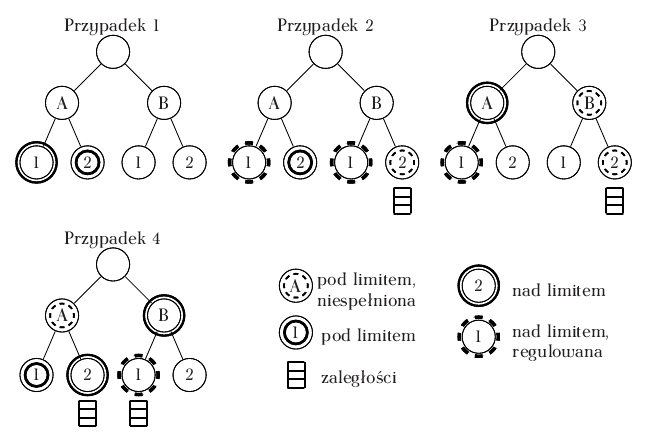Formalna zasada współdzielenia mówi, że

• klasa pozostaje nieregulowana jeśli nie jest nad limitem lub jeśli ma nieprzekraczającego limitu przodka na poziomie $i$, oraz nie ma niespełnionych klas w poddrzewie tego przodka na poziomie mniejszym niż $i$. W przeciwnym wypadku klasa jest regulowana.

1. Każda klasa jest spełniona – żadna nie musi byc regulowana.
2. Istnieją dwie klasy ponad ich limitem, ale tylko klasa $B2$ jest niespełniona, a użytkownik A nie jest nad limitem. Klasa $B1$ musi być regulowana z powodu klasy $B2$. Jednak obie interaktywne klasy będą w tym wypadku regulowane (W innym wypadku nieregulowana klasa $A1$ może doprowadzić to patologicznej sytuacji w której jedna z klas nie była by w stanie wysyłać żadnych danych; por. [2], dodatek C).
3. Użytkownik A jest nad limitem oraz jego klasa interaktywna jest nad limitem. Z kolei klasa $B2$ jest niespełniona. Klasa $A1$ musi być regulowana, ponieważ brany jest pod uwage stan limitu przodków.
4. Każda klasa-liść jest spełniona, ale klasa $A$ nie. Ponieważ jest ona pod limitem i nie istnieją niespełnione klasy niższego poziomu, klasa $A2$ może pozostać nieregulowana, natomiast klasa $B1$ będzie regulowana.

Do algorytmu wprowadzono też w ramach konfiguracji dodatkowe pojęcia klas uwolnionych (eng. exempt), związanych (ang. bounded) oraz izolowanych (ang. isolated).

• Klasa uwolniona – dostaje zawsze 100% udziału od planisty współdzielonego.
• Klasa związana – nie może pożyczać udziału od swoich przodków – dobry wybór dla klas interaktywnych, w których stabilność pasma jest ważniejsza niż czas reakcji,
• Klasa izolowana – nie pozwala pożyczać swojego niewykrozystanego przydziału innym klasom niż jej potomkom – opcja jest szczególnie przydatna w połączeniu z opcją uwolnienia

Aproksymacja formalnej zasady współdzielenia

W implementacji zasady współdzielenia napotyka się na problem sprawdzania czy któraś z klas w poddrzewie przodka jest niespełniona. Najprostszym rozwiązaniem jest ominięcie tego sprawdzania i założenie, że takich klas nie ma. Jest to zasada ,,tylko według przodków'' (ang. ancestor-only), która daje złe wyniki w niektórych sytuacjach, jak chociażby w przypadku $2$ z poprzedniego rysunku. Wyszukiwanie niespełnionych potomków można zrealizować dodając do sprawdzania przodków sprawdzanie ich poziomu oraz jego porównanie z globlaną zmienną $top\_level$.

• Klasa pozostaje nieregulowana jeśli jest pod limitem, lub jeśli ma przodka pod limitem, który ma $poziom \le top\_level$.

1. Jeśli pakiet zostanie zakolejkowany w klasie będącej pod limitem, to ustaw $top\_level = 1$
2. Jeśli $top\_level = i$ oraz pakiet zostanie zakolejkowany w klasie nad limitem, która posiada rodzica pod limitem oraz z poziomem $j < i$, to ustaw $top\_level = j$
3. Po wysłaniu pakietu z klasy, jeśli klasa ta nie ma już zaległości lub nie może kontynuować nieregulowana, ustaw $top\_level = \infty$

To heurystyczne postępowanie sprawia, że $top\_level$ jest ustawiany na $i$ tylko jeśli wiadomo, że istnieją klasy mogące wysłać dane bez pożyczania od przodka z poziomem wyższym od $i$. Obliczanie $top\_level$ wymaga troche czasu procesora, jednak jeśli zmienna ta zostanie ustawiona na $1$ to planista nie musi juz sprawdzac limitów rodzica, co kompensuje straty.

1. [^] David D. Clark, Van Jacobson, ,,Flexible and Efficient Resource Management for Datagram Networks'', rękopis, kwiecień 1991
2. [^] Sally Floyd, Van Jacobson, ,,Link-sharing and Resource Management Models for Packet Networks'', IEEE/ACM Transactions on Networking, Vol. 3 No. 4, sierpień 1995