AKKD

1. Dyscypliny, klasy, filtry
2. PRIO
3. CBQ
   1. Teoria
   2. Estymator i Planista
   3. Szczegóły implementacji
   4. Wykorzystanie
4. HTB
   1. Początki
   2. HTB 3
   3. Wykorzystanie
5. H-FSC
   1. Wstęp
   2. Krzywa usługi
   3. Sposób działania HFSC
   4. Deadline i Eligible time
   5. Virtual time
   6. Szczegóły implementacji
   7. Wykorzystanie

HTB 3

Po kilku nieudanych próbach[1], w 2002 roku HTB w wersji 3 dorównał szybkoscią CBQ. Udało się to kosztem przedefiniowania zasady współdzielenia przy pomocy inaczej określonych zmiennych, co jednak nie spowodowało spadku prezycji[2]. Przydzielmy klasom parametry:

• R (ang. rate – prędkość chwilowa)
• AR (ang. assured rate – prędkość gwarantowana),
• CR (ang. ceil rate – prędkość maksymalna),
• P (priorytet),
• level (poziom),
• Q (ang. quantum – kwant danych).
• mode– (tryb pracy, a umownie kolor) obliczany na podstawie $R$, $AR$, $CR$; przyjmuje następujące wartośći:
  • R (czerwona), jeśli $R > CR$ (klasa nie może wysyłać)
  • Y (żółta), jeśli $AR < R \le CR$ (klasa może pożyczać)
  • G (zielona), w pozostalych przypadkach (klasa może wysyłać)

Algorytm musi sterując przepływem dążyć do tego, by w każdej chwili dla każdej klasy $c$ było spełnione równanie: $$ R_c = \mathit{min}(CR_c, AR_c + B_c) $$ gdzie $B_c$ to pasmo pożyczone od przodków obliczane w następujący sposób (przy założeniu, że $p$ to rodzic $c$): $$ B_c = \frac {Q_c R_p} {\sum_{{i \in D(c):}\atop{P_i=C_i}} Q_i} ~~~\mathrm{jeśli}~~~ \mathit{min}_{i \in D(c)}(P_i) \ge P_c $$ $$ B_c = 0 ~~~\mathrm{w~przeciwnym~wypadku} $$ Jeśli klasa $c$ nie posiada rodzica (jest korzeniem), to $B_c = 0$. Dwie definicje pożyczania odzwierciedlają podział według priorytetu – kiedy istnieją potomkowie z zaległościami o wyższym piorytecie (numer priorytetu niższy) niż aktualnie rozpatrywana klasa, to nie możemy pożyczać ($B_c = 0$). Jeśli możemy, to pożyczmy od rodzica ułamek jego pasma ($R_p$) według przydzielonego nam kwantu ($Q_c$), biorąc wszytkie kwanty rodzeństwa o tym samym priorytecie jakos całość (mianownik). Definicje na $B_c$ oraz $R_c$ sa nawzajem rekursywne do momentu osiagnięcia korzenia. W wyniku przydzielania prędkości w oparciu o obliczenia według tych równań, $AR$ jest zapewniane każdej klasie, a nadmiar niewykorzystanego połączenia jest rozdzielany wagowo (na podstawie $Q$) potomkom mającym zaległości o tym samym priorytecie poczynając od nawyższego.

Ograniczenia które narzucają powyższe definicje są bardziej restrykcyjne niż zasada współdzielenia określona dla CBQ (), dlatego jeśli działanie algorytmu zgodne będzie z zasadami HTB, będzie też zgodne zasadami CBQ.

Struktura list w implementacji linuksowej HTB3.
Po prawej podajnik zewnętrzny wraz z listami białymi.
Przy każdej klasie nie będącej liściem – zbiór list z podajnika wewnętrznego.
W przykładzie występują dwa priorytety: czerwony – wysoki, niebieski – niski.
Według: M. Devera ,,Hierachical token bucket theory: HTB scheduler''.

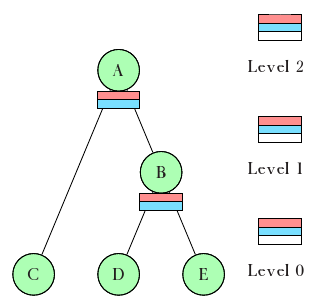Takie zdefiniowanie zasad wydaje się być juz proste w implementacji, pozostaje jedynie zagadnienie wyznaczania list $D(c)$. Implementacja HTB3, która pojawiłą się w Linuksie 2.4, utrzymuje dwa podajniki (rys.), z których pobierane są klasy: zewnętrzny (ang. self feed) oraz wewnętrzny (ang. inner feed). Podajnik zewnętrzny jest niezależny od hierarchi. Składa się z rodziny list, po jednym zbiorze na poziom. Każdy zbiór zawiera po jednej liście na priorytet. Każda lista w podajniku zewnętrznym zawiera zielone klasy (tzn. klasy w trybie zielonym), zgodne co do poziomu i priorytetu, które znajdują się w $D(c)$ dla pewnej klasy $c$.

Podajnik wewnętrzny opiera się na hierarchii klas; zawiera po jednym zbiorze dla każdej klasy nie będącej liściem. Zbiory te także składają się z list po jednej na priorytet. Listy ze zbioru przydzielonego do klasy $c$ zawierają żółte klasy znajdujące się w $D(c)$. Każda lista w tym slocie zawiera żółte klasy dla danego sobie priorytetu, które są potomkami $c$.

Obok podajnika zewnętrznego, istnieją też białe listy, po jednej na każdy poziom. Każda taka lista zwiera klasy z danego poziomu, które są czerwone lub żółte, posortowane według czasu w którym zmienią kolor.

Jeśli wszystkie klasy znajdują się na odpowiednich listach, to wybór tej, która następna powinna mieć możliwość wysłania danych jest prosty: należy znaleźć listę niepustą o najwyższym priorytecie, na najniższym poziomie. Na rysunku poniżej jest to lista czerwona na poziomie $0$, wysyłać więc może teraz klasa $D$. Na rysunku będzie to lista czerwona na poziomie $2$, a podążając listami z podajnika wewnętrznego wybrana zostanie także klasa $D$. Mimo, że klasa $E$ jest zielona, jednak nie ma ona nic do wysłania.

Przykładowe sytuacje w strukturze list HTB3.
Kolorowe i przerywane linie oznaczają przynależność do poszczególnych list.
Według: jw.

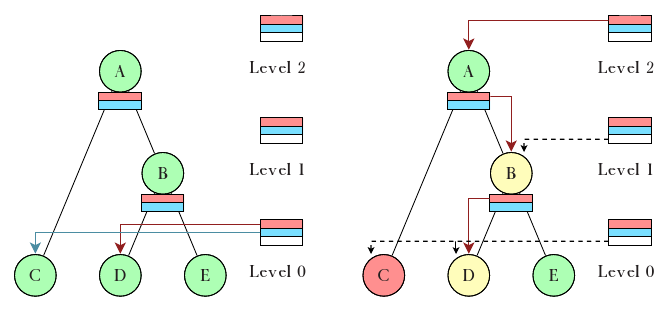Powiązania między listami zmieniają się jeśli jakaś klasa zmieni kolor. Ułatwiają to białe listy, gdyż nic nie zmieni się dopoki nie minie najbliższy czas spośród klas znajdujących się na głowach białych list. Jeśli powiązania wskazują na kilka klas równorzędnych co do priorytetu i poziomu na którym się znajdują, to klasy te są obsługiwane algorytmem DRR. Ciekawym aspektem struktury list HTB3 jest to, że podczas wyboru, kiedy odczytana zostanie biała lista danego poziomu i dokonane zostaną ewentualne zmiany w powiązaniach, można już wyszukać według podajników następną do obsłużenia klasę. Jeśli taka klasa zostanie wybrana, może zostać obsłużona bez sprawdzania białych list wyższych poziomów, gdyż jakakolwiek modyfikacja wyżej nie może doprowadzić do wybrania klasy na niższym poziomie (tylko taka miałaby pierwszeństwo).

Porównanie z CBQ

Algorytm HTB w wersji trzeciej okazał się nie wolniejszy niż CBQ [3] (Por. tabelka). Złożoność algorytmu skaluje się liniowo według prędkości łącza oraz ilości równocześnie aktywnych klas. Mimo iż istnieją ,,lepsze'' (jak to określił autor) algorytmy jak np. H-FSC, to jego mocną stroną jest zarówno iloczyn precyzji i szybkości działania jak i prostota konfiguracji.

1. [^] Por. M. Devera, ,,HTB 3 Linux queuing discipline developement''
2. [^] Por. M. Devera, ,,Hierachical token bucket theory''
3. [^] M. Devera, ,,HTB 3 performance compared''