AKKD

1. FIFO / FCFS
2. Round-robin - algorytm karuzelowy
3. Fair Queuing
4. Oryginalne SFQ - Stochastic Fair Queuing
5. Deficit Round-Robin
6. Linuksowe SFQ (Stochastic DRR)
7. RED - Losowe Wczesne Wykrywanie
8. Blue
9. SFB - Stochastyczny Sprawiedliwy RED
10. Wiadra
    1. Leaky bucket - Cieknące wiadro
    2. Token bucket - Wiadro żetonów

Deficit Round-Robin

W 1995 M. Shreedhar i G. Varghese zaproponował[1] odejście od modelu FQ, działającego w czasie $O(log(n))$ (z powodu konieczności sortowania pakietów po wirtualnym czasie; $n$ jest ilością połączeń) na rzecz pomysłu Deficytowego Algorytmu Karuzelowego (ang. Deficit Round-Robin – DRR) działąjącego w czasie $O(1)$, a więc możliwego do zaimplementowania sprzętowo w tanich urządzeniach sieciowych. Autorzy na nowo adresują problem nierównego podziału algorytmu karuzelowego w przypadku zmiennej wielkości pakietów.

Deficytowy algorytm karuzelowy. Dwa następujące po sobie momenty pierwszej rundy. $Q_i$ dla każdego połączenia wynosi $500$. Pakiet o wielkości $400$ mógł się więc wysłać; jednak pakiet o wielkości $600$ musi poczekac do drugiej rundy kiedy $DC$ jego połączenia wyniesie $2Q_i = 1000$.

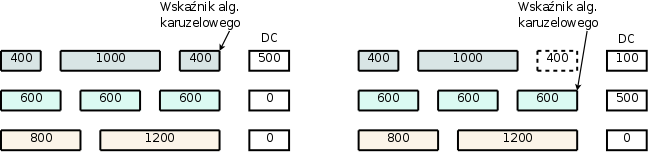Przypiszmy każdemu połączeniu wartość $Q_i$ przedstawiającą dozwoloną ilość bitów wysyłanych na jedną rundę algorytmu karuzelowego. Jakoże algorytm jest karuzelowy, możemy liczyć czas w ilości rund, czyli ilości iteracji po wszystkich połączeniach mających zaległości. Załóżmy na razie, że każdy strumień trafia do oddzielnej kolejki (tzn. algorytm nie jest stochastyczny). Określmy ilość wysłanych bitów z kolejki $i$ w rundzie $k$-tej jako $bits_i(k)$ (Autorowie algorytmu używają tutaj funkcji $bytes()$ porównując ją w zależnościach z funkcją $sent()$, a tą z kolei z wielkością $max$ liczoną w bitach. Jest to niekonsekwencja, która jednak nie ma wpływu na tok myślowy i wyniki analiz). Wprowadźmy wartość $DC_i$ będącą stanem kolejki $i$ i nazwaną licznikiem deficytu (ang. deficit counter), oznaczającą niewykorzystaną ilość bitów w danej rundzie. Deficytowy algorytm karuzelowy mówi, że w pierwszej rundzie, każde połączenie może wysłać ilość pakietów ograniczoną nierownością $bits_i(1) < Q_i$. Jeśli połączenie pozbyło się wszystkich pakietów z kolejki, to jego wartość $DC_i$ ustawiana jest na zero. W przeciwnym wypadku przyjmuje wartość $Q_i - bits_i(k)$. W kolejnych rundach każde połączenie może wysłać ilość pakietów ograniczoną nierownością $bits_i(k) < DC_i + Q_i$, po czym $DC_i$ przyjmuje wartość $DC_i + Q_i - bits_i(k)$ jeśli połączenie ma wciąż zaległośći, lub zero, w przeciwnym wypadku.

Szczegóły implementacji obejmują utrzymywanie tak zwanej aktywnej listy, która przechowuje jedynie kolejki aktualnie mające zaległości. Za każdym razem gdy nieaktywna kolejka otrzyma pakiet, jest ona wstawiana na koniec aktywnej listy. Algorytm karuzelowy obsługuje zawsze kolejkę z początku listy. Jeśli zostanie opróżniona – jest usuwana z listy, jeśli nie – przesuwana na koniec.

Z analizy działania DRR można wyprowadzić kilka dość istotnych stwierdzeń. W szczególności, DRR nie zbliża się maksymalnym opóźnieniem pojedynczego pakietu do algorytmu BR przy $Q_i$ dążącym do jedynki. Załóżmy, że istnieje $n$ kolejek, z czego $n-1$ kolejek ma zaległości w postaci pakietów wielkości $max$ bitów, a kolejka $n$-ta jest pusta. Wielkość $Q_i$ dla każdej kolejki wynosi $1$ bit. Algorytm nie wysyła więc nic przez $max-1$ rund, po których wartości $DC_i$ kolejek z zaległościami uzyskują wartość $max-1$. W tym momencie do ostatniej kolejki trafia pakiet wielkości $1$ bita. Zgodnie z algorytmem BR zostałby on wysłany po wysłaniu po jednym bicie z każdej z $n-1$ kolejek, czyli zostałby opóźniony o $n-1$ bitów. Jednak DRR będzie ustawiał $DC_i = max$ kolejno każdej kolejce z zakresu $(1,n-1)$, oraz wysyłał pakiet z niej zanim obsłuży ostatnią kolejkę z pakietem $1$-bitowym. Opóźnienie tego ostatniego wyniesie więc $(n-1) max$.

Do określenia gwarantowanej sprawiedliwości tego algorytmu potrzebne są dwa lematy (tamże, s. 379) ograniczające licznik deficytu oraz ilość wysłanych bitów:

• Lemat 1: Dla każdej kolejki $i$ i każdego czasu działania algorytmu DRR zachodzi $0 \le DC_i < max$, gdzie $max$ jest maksymalną wielkością pakietu.

Dowód: Wstępnie $DC_i = 0 \Rightarrow DC_i < Q_i$. $DC_i$ zmienia wartość tylko jeśli $i$ jest na początku aktywnej listy i jest obsługiwane przez wskaźnik algorytmu karuzelowego. Możliwe są wtedy dwie sytuacje:

• Jeśli jakiś pakiet pozostał w kolejce, to znaczy, że jest większy od $DC_i$, ponieważ każdy pakiet jest mniejszy lub równy $max$ to $DC_i < max$. Algorytm odejmuje od $DC_i$ tylko wartości od niego mniejsze lub równe, a więc $DC_i \ge 0$.
• Jeżeli żaden pakiet nie pozostał w kolejce, to $DC_i = 0$. ■
• Lemat 2: Dla każdego przedzialu czasu $(t_1, t_2)$, w którym kolejka $i$ ma zaległości, jeśli $m$ oznacza ilość rund w tym przedziale w których kolejka $i$ miała szansę być obsłużona, a $sent_i(k)$ – ilość wysłanych bitów od momentu $t_1$ do $k$-tej rundy włącznie ($sent_i(k) = \sum_{l=1}^k bits_i(l)$), to zachodzą nierówności: $$ m Q_i - max < sent_i(t_1, t_2) \le m Q_i + max $$

Dowód: Niech $DC_i(k)$ będzie wartością $DC_i$ w momencie zakończenia rundy $k$. Obserwacją wynikającą z działania algorytmu jest: $bits_i(k) + DC_i(k) = Q_i + DC_i(k-1)$. Korzystamy tu z założenia, że kolejka $i$ ma zaległości w całym przedziale $(t_1, t_2)$ (inaczej $DC_i$ zostałoby w pewnym momencie wyzerowane). Przekształcając to równanie w $bits_i(k) = Q_i + DC_i(k-1) - DC_i(k)$ i sumując po całym okresie $(t_1, t_2)$, czyli przez $m$ rund, otrzymujemy sumę teleskopową: $$sent_i(m) = m Q_i + DC_i(0) - DC_i(m)$$ Równanie to dowodzi lematu po uwzględnieniu ograniczeń na $DC_i$ narzuconych przez Lemat 1. ■

• Twierdzenie o DRR: Dla każdego przedziału czasu $(t_1, t_2)$, DRR zapewnia sprawiedliwość $FM(t_1, t_2) \le Q + 2 max$, gdzie $Q$ jest najmniejszym $Q_i$ spośród wszystkich kolejek aktualnie mających zaległości.

  Dowód: Wybierzmy dowolne dwie kolejki $i$, $j$ mające zaległości w przedziale $(t_1, t_2)$. Zgodnie z działaniem algorytmu karuzelowego oraz sposobem implementacji aktywnej listy, skoro w danym przedziale czasu $i$ oraz $j$ mają zaległości to pomiędzy dwiema szansami kolejki $i$ na wysłanie pakietu, kolejka $j$ miała jedną swoją szansę. Niech $m$ będzie ilością szans kolejki $i$ w przedziale $(t_1, t_2)$, a $m'$ ilością takich szans kolejki $j$. Wtedy $|m - m'| \le 1$.

  Wprowadźmy $f_i = \frac{Q_i}{Q}$, interpretowane jako wielkość przydziału łącza dla połączenia $i$. Z Lematu 2 dla kolejki $i$ mamy (1): $$sent_i(t_1, t_2) \le m Q_i + max$$ $$sent_i(t_1, t_2) \le (m-1) Q_i + Q_i + max$$ $$\frac{sent_i(t_1, t_2)}{f_i} \le (m-1) Q + Q + \frac{max}{f_i}$$

  Natomiast dla kolejki $j$ możemy zastosować Lemat 2 w ten sposób (2): $$sent_j(t_1, t_2) \ge m' Q_j - max$$ $$\frac{sent_j(t_1, t_2)}{f_j} \ge m' Q - \frac{max}{f_j}$$

  Odejmując (2) od (1) i uwzględniając nierówność $m' \ge m-1$ otrzymujemy: $$\frac{sent_i(t_1,t_2)}{f_i} - \frac{sent_j(t_1,t_2)}{f_j} \le Q + \frac{max}{f_i} + \frac{max}{f_j}$$ Lewa strona tego równania to $FM(t_1,t_2)$, a ponieważ $f_i$ i $f_j$ są $\ge 1$, to $$FM(t_1,t_2) \le Q + \frac{max}{f_i} + \frac{max}{f_j} \le Q + 2 max$$ ■

Autorzy algorytmu pokazują też, że przy uzyciu funkcji haszującej (brak porównań), listy aktywnej (brak iteracji) oraz wszystkich $Q_i \ge max$ (w każdej rundzie każde połączenie wysyła przynajmniej jeden pakiet) algorytm wykonuje się w stałej liczbie operacji, a więc jego złożoność wynosi w najgorszym przypadku $O(1)$. Jeśli weźmiemy pod uwagę, że przy wykorzystaniu funkcji haszującej czasami zdarzają się kolizje, to złożoność ta jest i tak oczekiwana. Można więc napisać, że przy optymalnej wydajności ($Q = Max$), DRR gwarantuje sprawiedliwość $FM = 3 max$.

Implementacja i zastosowanie (w linuksowym sfq)

1. [^] M. Shreedhar, George Varghese, ,,Efficient fair queueing using deficit round robin'', ACM SIGCOMM Computer Communication Review 25 (4), 1995