r =
s =
ss =
Bezklasowe / Wiadra / Token bucket - Wiadro żetonów: Teoria — Implementacja — Wykorzystanie

Token bucket - Wiadro żetonów

Podobnym pomysłem (często wzajemnie mylonym) jest wiadro żetonów (ang. token bucket). Do wiadra wpadają żetony w stałym tempie (odpowiednik $\rho$ z wersji cieknącej). Kiedy wiadro się zapełni, napływające żetony są odrzucane. Każdy żeton reprezentuje pozwolenie na wysłanie określonej ilości bitów. Aby wysłać pakiet, wymagana jest ilość żetonów odpowiadająca bitowo wielkości pakietu. Po wysłaniu pakietu ,,wykorzystane'' żetony są usuwane z wiadra. Jeśli brak jest wystarczającej ilości żetonów – pakiet, w zależności od implementacji, czeka, jest zaznaczany lub odrzucany. Żetony odrzucone ze względu na przepełenie wiadra nie mogą już być wykorzystane do wysyłania pakietów. Zatem maksymalna możliwa fala wysyłanych pakietów jest proporcjonalna do wielkości wiadra.

Głównym atutem w porównaniu z cieknącym wiadrem jest możliwość chwilowego wysłania większej ilości danych jeśli bezpośrednio wczesniej przepustowość wiadra nie była wykorzystywana w pełni. Innymi słowy, przez pewien czas (zależny od wielkości wiadra oraz jego zapełniena żetonami) pakiety mogą być wysyłane bez ograniczeń. Aby obliczyć maksymalny czas $t$ w którym wiadro żetonów pozwala wysyłać bez ograniczeń, oznaczmy tempo nadsyłania żetonów jako $\rho$ bit/s. Zakładamy, że wiadro w momencie rozpoczęcia wysyłania jest pełne żetonów, czyli mamy do dyspozycji $\sigma$ bitów – pojemność wiadra. Wysyłanie to odbywa się z maksymalną możliwą prędkością $m$ (oczywiście $\rho \le m$). Oprócz wysłania $\sigma$ bitów, wyślemy też tyle, ile w tym czasie napłynie nowych żetonów (z prędkością $\rho$). Zachodzi więc następująca równość: $$\sigma + \rho t = m t$$ $$t = \frac{\sigma}{m-\rho}$$

Warto zaznaczyć, że mimo pozwolenia na chwilowe przekroczenie przepustowości $\rho$, ograniczenie przepływności dla wiadra żetonów można określić identycznie jak dla cieknącego wiadra (wzory 1, 2).

Implementacja

Wiadro żetonów zostało zaimplementowane[1] w Linusie 2.2 jako TBF (Token Bucket Filter) przez Alexey'a Kuznetsova. Algorytm działa w następujący sposób (rys.): Niech $N(t_1) = \frac{\sigma}{\rho}$ oraz niech rośnie w czasie według równania $$N(t+\Delta) = min \left\{ \frac{\sigma}{\rho}, N(t) + \Delta \right\}$$ Jeśli pierwszy pakiet ma wiekość $s$, to może być wysłany tylko w czasie $t_x$ jeśli $\frac{s}{\rho} \le N(t_x)$, i jeśli tak się stanie, to $$N(t_x + \delta) = N(t_x - \delta) - \frac{s}{\rho}$$ gdzie $\delta \rightarrow 0$.

Schemat działania TBF na podstawie przebiegu funkcji $N(t)$. Początkowo $N(t) = \sigma / \rho = 5$.
W momencie $t=3$ oraz $t=4$ przychodą pakiety odpowiednio $s_1$ i $s_2$,
jednak pakiet $s_2$ został wstrzymany do $t=5$ z powodu braku żetonów.

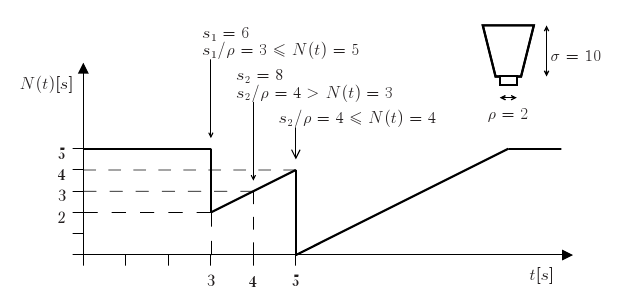Algorytm oparty o wiadro żetonów rzadko jest stosowany bezpośrednio, a częściej wewnątrz większych algorytmów jak na przykład HTB.

Podsumowując, różnica między cieknącym wiadrem a wiadrem żetonów polega na tym, że to pierwsze przetrzymuje (opóźnia) chwilowy nadmiar danych, a to drugie pozwala mu wykorzystać przez pewien czas dodatkowe pasmo. Po przekroczeniu przez nadmiar danych ustalonego limitu, jedno i drugie zaczyna odrzucać pakiety. Oba wiadra pozwalają też na precyzyjne ustalenie przepustowości, przy czym tylko cieknące wiadro nigdy jej nie przekroczy.

Wykorzystanie

TBF przyjmuje następujące parametry:

  • limit/latency — maksymalna ilość pakietów oczekujących równocześnie na przydział żetonu; jeśli zostanie przekroczona — nadmiarowe pakiety będą odrzucane. Ma to bezpośredni związek z maksymalnym możliwym opóźnieniem pakietu w kolejce, dlatego możliwe jest również podanie tego opóźnienia parametrem latency. Nie można podawać tych dwóch opcji razem, gdyż wykluczają się one wzajemnie;
  • burst — wielkość wiadra, tzn. ilość bajtów jaką równocześnie mogą pomieścić żetony;
  • mpu — wielkość pustego pakietu; standardowo w sieciach jest to 64 bajty, brak tego parametru ustawia jednap mpu na 0 bajtów więc warto ten parametr podać;
  • rate — prędkość nadsyłania żetonów (w bajtach na sekunde).

Wedug man tc-tbf aby utrzymać na interfejsie prędkość 0.5mbit/s, dopuszczać 5 kilobajtowe przypływy z prędkością maksymalną 1.0mbit/s oraz zapewnić maksymalne opóźnienie 70ms: 

tc qdisc add dev eth0 root tbf rate 0.5mbit burst 5kb latency 70ms peakrate 1mbit minburst 1540 mpu 64

Możemy zasymulować modem z łączem o prędkości wysyłania 8mbit i dużym buforze (limit 50 pakietów = 77kb przy transferach z maksymalną wielkością pakietów) poleceniem: 

tc qdisc add dev eth0 root handle 1: tbf rate 10mbit burst 5kb limit 77kb minburst 1540 mpu 64
Podczas transferu wysycającego łącze opóźnienia wzrastają do około 70ms. Po przejściu przez kolejkę modemu można wykorzystać tbf do redukcji opóźnienia (tzn. nie pozwolić na zapełnienie się bufora w modemie). Aby to zasymulować pod stworzoną kolejkę (parent 1:) podpinamy nową kolejkę, która ograniczy maksymalne opóźnienie do 5ms. 
tc qdisc add dev eth0 parent 1: tbf rate 7.5mbit burst 5kb latency 5ms minburst 1540 mpu 64
Teraz opóźnienie powinno utrzymywać się na poziomie 6ms. Wydając polecenie 
tc qdisc ls dev eth0
można zauważyć przy pierwszej kolejce obliczone lat 73ms, co potwierdza pierwsze obserwacje.

Przypisy

  1. [^] linux/net/sched/sch_tbf.c

Creative Commons License Content by Michał Pokrywka is licensed under a Creative Commons BY-SA 3.0
Ostatnia znacząca zmiana: 2010-04-28