r =
s =
ss =

AKKD

Nowości Historia i teoria : : Algorytmy bezklasowe : : Algorytmy klasowe : : Klasyfikowanie ruchu (filtry) : : Dobre praktyki

Bezklasowe / Fair Queuing: Teoria

Fair Queuing

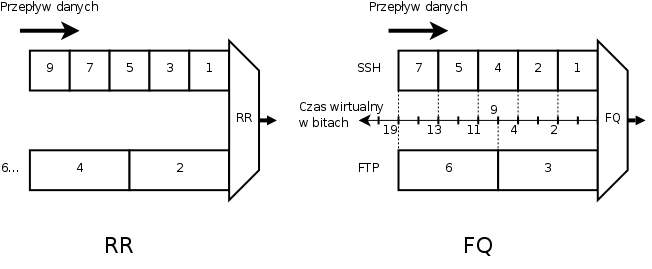
Jeżli mamy dwa połączenia, z których jedno przesyłą dwa razy większe pakiety, a algorytm karuzelowy obsługiwać będzie po jednym pakiecie z każdego połączenia, to w każdym okresie drugie połączenie wyśle ponad dwa razy więcej bitów. Jest to podstawowy problem algorytmu dzielącego pasmo pakietowo. Rozwiązaniem problemu zmiennej długości pakietów byłoby dzielenie pasma bitowo, np. wysyłanie określonej ilość bitów z każdego połączenia. Niestety protokół IP wymaga wysylania całego pakietu na raz. Algorytm sprawiedliwego kolejkowania (ang. Fair Queuing) emuluje dzielenie bitowe obliczając kiedy każdy pakiet powinien zostać wysłany, by czasy pokrywały się (czy też były jak najbardziej zbliżone) z wysłaniem ostatniego bitu pakietu przez domniemany algorytm karuzelowy dzielący bitowo.

Obliczanie rzeczywistych czasów wysyłania pakietów jest wykonalne jednak bardzo pracochłonne. Dane o czasach musiałyby być przeliczane po każdym wysłaniu pakietu oraz po każdym zakolejkowaniu nowego pakietu.

Około 1990 roku panowie Demers, Keshav i Shenker na podstawie pomysłu [1] Johna Nagle'a zaproponowali [2] inny sposób obliczania czasów wysyłania pakietów. Stworzyli oni model (dalej: model FQ) czasu wirtualnego na podstawie hipoptetycznego algorytmu karuzelowego dzielącego bitowo (dalej: BR – Bit-by-bit Round-robin). Konkretnie rzecz biorąc, algorytm BR w każdym swoim przebiegu wysyła z każdej kolejki po jednym bicie.

Porównanie działania algorytmu karuzelowego (RR) i FQ.
Do kolejki trafiają pakiety z dwóch sesji (powiedzmy SSH (2-bitowe) i FTP (5-bitowe)).
Numery na pakietach wyznaczają kolejność wysyłania,
a wartości na osi czasu wirtualnego ilość wysłanych bitów.

Wprowadźmy następujące oznaczenia:

$R(t)$ – ilość zakończonych przebiegów jakie wykonał algorym BR do czasu $t$,
$N_{ac}(t)$ – ilość aktywnych połączeń (tych mających w kolejce jakieś pakiety do wysłania) w chwili $t$,
$\mu$ – ilość wysyłanych bitów w jednostce czasu; dla uproszczenia przyjmijmy, że $\mu = 1$.

Zachodzi następująca zależnośc: $\frac{\delta R}{\delta t} = \frac{\mu}{N_{ac}(t)}$. Pakiet o wielkości $P$ bitów, którego pierwszy bit zostanie wysłany o czasie $t_0$, zostanie wysłany do końca $P$ przebiegów później (zostanie wtedy wysłany jego ostatni bit), oznaczmy ten czas jako $t$. Zatem $R(t) = R(t_0) + P$. Jeśli oznaczmy dodatkowo:

$t^\alpha_i$ – czas kiedy pakiet $i$ z połączenia $\alpha$ nadszedł (został zakolejkowany),
$S^\alpha_i$ – wartość $R(t)$ kiedy wysłany został pierwszy bit pakietu (rozpoczęcie wysyłania),
$F^\alpha_i$ – zakończenie wysyłania pakietu,
$P^\alpha_i$ – wielkość pakietu,

to prawdziwe są równania: $$ F^\alpha_i = S^\alpha_i + P^\alpha_i ~~~ ~~~ ~~~ S^\alpha_i = \max(F^\alpha_{i-1}, R(t^\alpha_i)) $$ Skoro $R(t)$ jest funkcją rosnącą, zwiększającą swoją wartość za każdym razem kiedy czekają jakieś bity do wysłania, to kolejność $F^\alpha_i$ odpowiada kolejności czasów rzeczywistych kończenia wysyłania pakierów w algorytmie BR.

Można zauważyc, że $R(t)$ i $N_{ac}(t)$ oraz $S^\alpha_i$ i $F^\alpha_i$ zależą tylko od czasów nadejścia ($t^\alpha_i$) a nie rozpoczęcia lub zakończenia wysyłania pakietu jesli tylko ustalimy, że połączenie jest aktywne kiedy $R(t) \le F^\alpha_i$ dla $i=\max_j(t^\alpha_j \le t)$. Możemy się więc tymi wartościami posługiwać w algorytmie wysyłającym całe pakiety na raz. Algorytm implementujący FQ powinien wysyłać zawsze pakiet o najmniejszym $F^\alpha_i$, dążąc do redukcji rozbieżności pomiędzy wszystkimi czasami wirtualnymi. Zauważmy, że jest to zgodne z twierdzeniem o dodatkowym małym przydziale (o którym było tutaj).

Pojawia się tutaj kwestia decyzji co zrobić, kiedy aktualnie wysyłany pakiet ma większą (,,późniejszą'') wartość $F^\alpha_i$ od pakietu który dopiero co nadszedł (tzn. po rozpoczęciu wysyłania poprzedniego pakietu). Można wtedy zatrzymać wysyłanie aktualnego pakietu i wysłać ten z mniejszym $F^\alpha_i$ (jest to algorytm FQ prewencyjny/preemptive), lub możemy kontynuować wysyłanie pozwalając na małą niezgodność w kolejności wartości $F^\alpha_i$ (jest to algorytm FQ nie-prewencyjny/non-preemptive). Algorytm prewencyjny jest przyjazny dla połączeń interaktywnych, jednak część przepustowości jest marnowana razem z przerwaniem niedokońca wysłanego pakietu. W praktyce różnice te są na tyle małe, że w rozważaniach teoretycznych korzysta się z algorytmu prewencyjnego, a implementuje ten drugi. Dokładność FQ zbliża się asymptotycznie do BR wraz z długością trwania połączenia.

W rzeczywistości do algorytmu FQ dodany jest współczynnik faworyzujący połączenia nieaktywne. Kolejność pakietów wybierana jest na podstawie wartości obliczanej nieco inaczej niż $F^\alpha_i$. Mianowicie jest to $B^\alpha_i = P^\alpha_i + \max(F^\alpha_{i-1}, R(t^\alpha_i) - \delta)$, gdzie $\delta$ jest współczynnikiem faworyzowania niekatywnych połączeń. Należy bowiem zauważyć, że druga wartość z funkcji max jest wybierana właśnie wtedy, kiedy wirtualny czas $F^\alpha_i$ już minął ($R(t)$ jest niejako ,,wirtualną teraźniejszością''), a więc ostatni pakiet tej sesji został już wysłany.

Ostatnim niuansem o którym należałoby wspomnieć jest problem przeciążenia bufora interfejsu sieciowego. Algorytm FQ w tym wypadku usuwa ostatnio zakolejkowany pakiet z sesji, która w danej chwili ma najwięcej bitów w swojej kolejce. Może się oczywiście zdarzyć (i jest to najbardziej prawopodobne), że będzie to właśnie pakiet który spowodował przepełnienie.

Przypisy

Content by Michał Pokrywka is licensed under a Creative Commons BY-SA 3.0
Ostatnia znacząca zmiana: 2010-04-28