AKKD

1. Gra wieloosobowa
2. Teoria sprawiedliwości
   1. Pomiar sprawiedliwości (fairness measure)
   2. Pomiar Golestaniego
   3. Sprawiedliwość minimaksymalna (min-max fairness)
3. Problematyczne sytuacje
4. Globalna synchronizacja
5. Jakość usług (QoS)

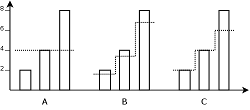
Sprawiedliwość minimaksymalna

Podział pasma określa się jako sprawiedliwy minimaksymalnie jeśli: po pierwsze, przepływ o najmniejszej prędkości jest zmaksymalizowany, po drugie, przepływ o drugiej najmniejszej prędkości jest zmaksymalizowany, i tak dalej. (Wersja bardziej formalna jest mało czytelna [1])

Aby zobrazować tą niezbyt zwięzłą definicję, na rysunku przedstawione zostało porównanie podziałów idealnych wg trzech metod razem z podziałem minimaksymalnym, a w tabeli wskaźniki sprawiedliwości dla tych podziałów. Wskaźniki obliczane dla podziału tego samego rodzaju uzyskują oczywiście wartość 1 (podział idealnie sprawiedliwy).

Podział minimaksymalny gwarantuje każdemu połączeniu, że otrzyma ono nie mniej niż $C/n$ przydziału, gdzie $C$ to całość zasobu, a $n$ to ilość połączeń. Jeśli któreś połączenie wymaga mniej iż $C/n$ przydziału, wtedy nadmiar trafia równomiernie do reszty połączeń. Tak zdefiniowana sprawiedliwość została szeroko uznana za optymalną. Trudno ją jednak zaimplementować w realnym środowisku, gdzie zapotrzebowanie zmienia się dynamicznie.

Reasumując, wskaźnik sprawiedliwości oraz wskaźnik Golestaniego jest optymalny jeśli przydziały sa normalizowane ograniczeniami administracyjnymi (każdy powinien otrzymać równy ułamek swojego maksymalnego przydziału), a wskaźnik sprawiedliwości z minimaksymalnym przydziałem idealnym jako zapotrzebowanie jest optymalny jeśli przydziały są normalizowane aktualnym zapotrzebowaniem.

1. [^] Jean-Yves Le Boudec, ,,Rate adaptation, Congestion Control and Fairness: A Tutorial'', Ecole Polytechnique Fédérale de Lausanne, grudzień 2008, s. 8